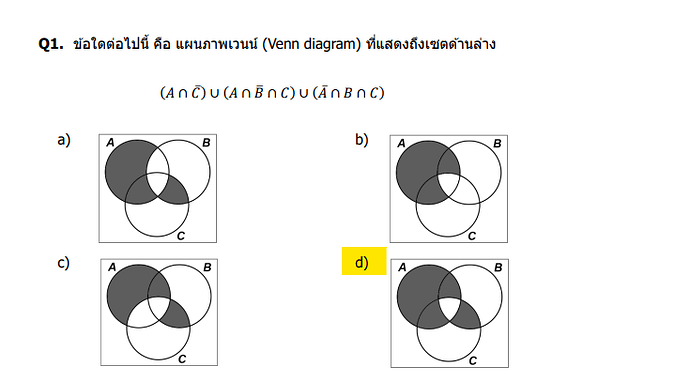
2023S_FE_AM_Answer.pdf (40.4 KB)
2023S_FE_AM_Questions.pdf (528.9 KB)
2023S_FE_AM_Questions_Thai.pdf (789.7 KB)
A = 1010
B = 1011
C = 1100
D = 1101
ABCD (hex) = 1010 1011 1100 1101 (16 บิต)
ขั้นที่ 2: ขยายให้เต็ม 32 บิต (เติม 0 ข้างหน้า)
0000 0000 0000 0000 1010 1011 1100 1101
ขั้นที่ 3: ทำ Logical Right Shift 2 บิต
Logical right shift = เลื่อนบิตไปทางขวา และเติม 0 ทางซ้าย
ก่อนเลื่อน: 0000 0000 0000 0000 1010 1011 1100 1101
↓↓ (สองบิตนี้จะหลุดออกไป)
หลังเลื่อน: 00|00 0000 0000 0000 0010 1010 1111 0011
↑↑ (เติม 0 สองบิตเข้ามา)
ขั้นที่ 4: แปลงกลับเป็นเลขฐานสิบหก
0000 0000 0000 0000 0010 1010 1111 0011
0 0 0 0 2 A F 3
สูตรลัด
การ shift ขวา 2 บิต = หารด้วย 2² = หารด้วย 4
ABCD (hex) ÷ 4 = ?
ABCD = 43981 (decimal)
43981 ÷ 4 = 10995.25 → เอาเฉพาะจำนวนเต็ม = 10995
10995 (decimal) = 2AF3 (hex)
วิเคราะห์โจทย์
- โยนเหรียญ 4 เหรียญ พร้อมกัน
- หาความน่าจะเป็นที่จะได้ อย่างน้อย 3 เหรียญขึ้นหัว
ขั้นตอนการแก้
ขั้นที่ 1: หาจำนวนผลลัพธ์ทั้งหมด
เมื่อโยนเหรียญ 4 เหรียญ แต่ละเหรียญมี 2 ผลลัพธ์ (หัว/ก้อย)
จำนวนผลลัพธ์ทั้งหมด = 2⁴ = 16 วิธี
ขั้นที่ 2: หาจำนวนผลลัพธ์ที่ต้องการ
“อย่างน้อย 3 เหรียญขึ้นหัว” หมายถึง:
- 3 เหรียญขึ้นหัว, 1 เหรียญขึ้นก้อย หรือ
- 4 เหรียญขึ้นหัวทั้งหมด
กรณีที่ 1: 3 หัว, 1 ก้อย
จำนวนวิธี = C(4,3) = 4!/[3!(4-3)!] = 4 วิธี
ได้แก่:
- H H H T
- H H T H
- H T H H
- T H H H
กรณีที่ 2: 4 หัว, 0 ก้อย
จำนวนวิธี = C(4,4) = 1 วิธี
ได้แก่:
- H H H H
ขั้นที่ 3: คำนวณความน่าจะเป็น
จำนวนผลลัพธ์ที่ต้องการ = 4 + 1 = 5 วิธี
ความน่าจะเป็น = จำนวนผลลัพธ์ที่ต้องการ / จำนวนผลลัพธ์ทั้งหมด
= 5/16
คำตอบ: b) 5/16 
วิเคราะห์โจทย์
- Random(n) คืนค่าจำนวนเต็มตั้งแต่ 0 ถึง n-1 (รวม n ค่า) แบบ uniform probability
- A = Random(10) → A มีค่าได้: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 (10 ค่า)
- B = Random(10) → B มีค่าได้: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 (10 ค่า)
- C = A - B
- หา P(C = 0)
## ขั้นตอนการแก้
**ขั้นที่ 1:** หาเงื่อนไขที่ทำให้ C = 0
C = 0
A - B = 0
A = B
**ขั้นที่ 2:** หาจำนวนผลลัพธ์ทั้งหมด
เนื่องจาก A และ B เป็นตัวแปรสุ่มอิสระ:
จำนวนผลลัพธ์ทั้งหมด (A, B) = 10 × 10 = **100 คู่**
**ขั้นที่ 3:** หาจำนวนกรณีที่ A = B
กรณีที่ A = B:
- (0, 0)
- (1, 1)
- (2, 2)
- (3, 3)
- (4, 4)
- (5, 5)
- (6, 6)
- (7, 7)
- (8, 8)
- (9, 9)
มีทั้งหมด **10 คู่**
**ขั้นที่ 4:** คำนวณความน่าจะเป็น
P(C = 0) = P(A = B) = จำนวนกรณีที่ A = B / จำนวนผลลัพธ์ทั้งหมด
P(C = 0) = 10/100 = 1/10
## **คำตอบ: c) 1/10** ✅
### หมายเหตุ
ในการเขียนโปรแกรม ฟังก์ชัน Random(n) มักหมายถึง:
* **Python:** `random.randrange(n)` → คืนค่า 0 ถึง n-1
* **Java:** `Random.nextInt(n)` → คืนค่า 0 ถึง n-1
* **JavaScript:** `Math.floor(Math.random() * n)` → คืนค่า 0 ถึง n-1

คำตอบและวิธีทำ
วิเคราะห์ BNF Grammar
<number> ::= 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9
<letter> ::= A | B | C | D | E | F
<letter-and-number> ::= <letter> | <number> | _
<variable-name> ::= <letter> | <variable-name><letter-and-number>
## กฎสำคัญ
จากกฎที่ 4: `<variable-name> ::= <letter> | <variable-name><letter-and-number>`
**ความหมาย:**
- **ตัวแรกต้องเป็น `<letter>` เท่านั้น** (A, B, C, D, E, หรือ F)
- ตัวถัดไปสามารถเป็น `<letter-and-number>` ได้ (A-F, 0-9, หรือ _)
## ตรวจสอบแต่ละตัวเลือก
### a) _B39 ❌
- เริ่มต้นด้วย `_` (underscore)
- `_` **ไม่ใช่** `<letter>`
- ละเมิดกฎ: ต้องเริ่มด้วยตัวอักษร
- **ไม่ถูกต้อง**
### b) 246 ❌
- เริ่มต้นด้วย `2` (ตัวเลข)
- `2` **ไม่ใช่** `<letter>`
- ละเมิดกฎ: ต้องเริ่มด้วยตัวอักษร
- **ไม่ถูกต้อง**
### c) 3E5 ❌
- เริ่มต้นด้วย `3` (ตัวเลข)
- `3` **ไม่ใช่** `<letter>`
- ละเมิดกฎ: ต้องเริ่มด้วยตัวอักษร
- **ไม่ถูกต้อง**
### d) F5_1 ✅
- ตัวที่ 1: `F` → เป็น `<letter>` ✓
- ตัวที่ 2: `5` → เป็น `<number>` ซึ่งอยู่ใน `<letter-and-number>` ✓
- ตัวที่ 3: `_` → อยู่ใน `<letter-and-number>` ✓
- ตัวที่ 4: `1` → เป็น `<number>` ซึ่งอยู่ใน `<letter-and-number>` ✓
- **ถูกต้องทุกข้อ**
## การ Derive (พิสูจน์)
<variable-name>
→ <variable-name><letter-and-number> [F5_]
→ <variable-name><letter-and-number><letter-and-number> [F5]
→ <letter><letter-and-number><letter-and-number><letter-and-number>
→ F · 5 · _ · 1
คำตอบ: d) F5_1 
สรุป
Variable name ที่ถูกต้องตาม BNF นี้:
- ✓ ต้องเริ่มด้วยตัวอักษร A-F
- ✓ ตามด้วยตัวอักษร, ตัวเลข, หรือ _ ได้
- ✗ ห้ามเริ่มด้วยตัวเลขหรือ underscore

คำตอบและวิธีทำ
วิเคราะห์โจทย์
โจทย์อธิบายวิธีการตรวจจับข้อผิดพลาดที่มีลักษณะ:
- ข้อมูลที่ส่งมาพร้อมกับเศษที่เหลือจากการหาร ข้อมูลด้วยพหุนาม (Generator polynomial)
- ผู้รับจะตรวจสอบ โดยการหารข้อมูลด้วยพหุนามชุดเดียวกัน
- ใช้ชุดที่เหลือมาตรวจสอบความถูกต้อง
วิเคราะห์แต่ละตัวเลือก
a) CRC (Cyclic Redundancy Check) 
หลักการทำงาน:
ฝั่งส่ง:
1. เอาข้อมูล (Data) หารด้วย Generator Polynomial
2. ได้เศษเหลือ (Remainder) = CRC
3. ส่ง: Data + CRC
ฝั่งรับ:
1. เอา (Data + CRC) ที่ได้รับ หารด้วย Generator Polynomial เดียวกัน
2. ถ้าเศษเหลือ = 0 → ข้อมูลถูกต้อง
3. ถ้าเศษเหลือ ≠ 0 → มี error
ตัวอย่าง:
- Generator Polynomial: x³ + x + 1 → 1011 (binary)
- Data: 1101
- คำนวณ CRC แล้วแนบท้าย
- ตรงกับคำอธิบายในโจทย์ทุกประการ
b) Hamming code 
- เป็น Error Correcting Code (แก้ไข error ได้)
- ใช้การคำนวณ parity bits หลายตัว
- ไม่ได้ใช้ Generator Polynomial
- ไม่ตรงกับโจทย์
c) Horizontal parity check 
- ตรวจสอบความสมดุล (parity) ในแนวนอน
- คำนวณ XOR ของบิตในแต่ละแถว
- ไม่ได้ใช้ Generator Polynomial
- ไม่ตรงกับโจทย์
d) Vertical parity check 
- ตรวจสอบความสมดุล (parity) ในแนวตั้ง
- คำนวณ XOR ของบิตในแต่ละคอลัมน์
- ไม่ได้ใช้ Generator Polynomial
- ไม่ตรงกับโจทย์
ตัวอย่าง CRC Calculation
ให้:
- Data = 1101
- Generator = 1011 (x³ + x + 1)
ขั้นตอน:
1100 ← Quotient (ไม่สนใจ)
-------
1011 | 1101000 ← Data + 3 bits (000)
1011
----
0100
0000
----
1000
1011
----
0110 ← Remainder (CRC)
ส่งข้อมูล: 1101 + 011 = 1101011
คำตอบ: a) CRC 
สรุปจุดสำคัญ
CRC คือวิธีเดียวที่:
- ใช้ Generator Polynomial ในการคำนวณ
- ส่งข้อมูลพร้อมเศษที่เหลือ (remainder)
- ผู้รับตรวจสอบโดยการหารด้วย polynomial เดียวกัน
- ใช้กันอย่างแพร่หลายใน: Ethernet, WiFi, USB, Storage devices
คำตอบและวิธีทำ
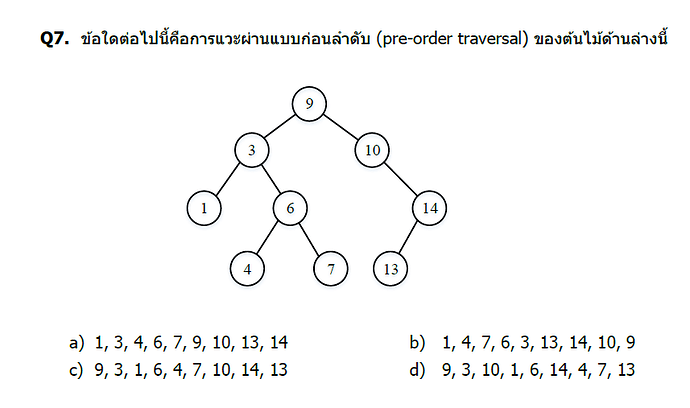
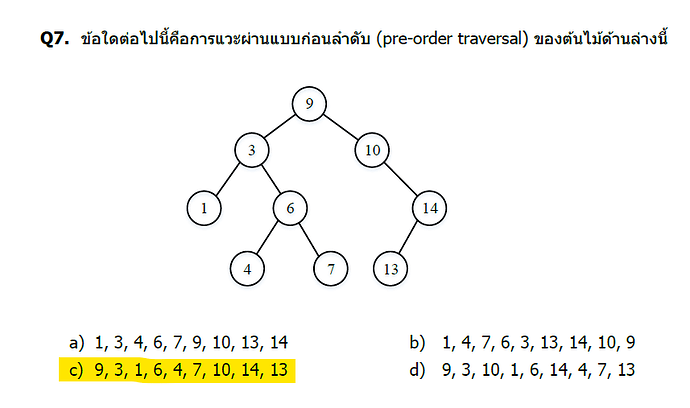
หลักการ Pre-order Traversal
Pre-order traversal มีลำดับ: Root → Left → Right
กฎ:
- เยี่ยมชม โหนดปัจจุบัน ก่อน
- ไป subtree ซ้าย ทั้งหมด
- ไป subtree ขวา ทั้งหมด
โครงสร้างต้นไม้
9 (root)
/ \
3 10
/ \ \
1 6 14
/ \ /
4 7 13
ขั้นตอนการเดินผ่าน
ขั้นที่ 1: เริ่มที่ Root
- เยี่ยม 9 ✓
- ลำดับ:
9
ขั้นที่ 2: ไป Left subtree ของ 9 (คือ 3)
- เยี่ยม 3 ✓
- ลำดับ:
9, 3
ขั้นที่ 3: ไป Left subtree ของ 3 (คือ 1)
- เยี่ยม 1 ✓ (ไม่มี children)
- ลำดับ:
9, 3, 1
ขั้นที่ 4: ไป Right subtree ของ 3 (คือ 6)
- เยี่ยม 6 ✓
- ลำดับ:
9, 3, 1, 6
ขั้นที่ 5: ไป Left subtree ของ 6 (คือ 4)
- เยี่ยม 4 ✓ (ไม่มี children)
- ลำดับ:
9, 3, 1, 6, 4
ขั้นที่ 6: ไป Right subtree ของ 6 (คือ 7)
- เยี่ยม 7 ✓ (ไม่มี children)
- ลำดับ:
9, 3, 1, 6, 4, 7
ขั้นที่ 7: เสร็จ Left subtree ของ 9 แล้ว, ไป Right subtree (คือ 10)
- เยี่ยม 10 ✓
- ลำดับ:
9, 3, 1, 6, 4, 7, 10
ขั้นที่ 8: ไป Right subtree ของ 10 (คือ 14)
- เยี่ยม 14 ✓
- ลำดับ:
9, 3, 1, 6, 4, 7, 10, 14
ขั้นที่ 9: ไป Left subtree ของ 14 (คือ 13)
- เยี่ยม 13 ✓ (ไม่มี children)
- ลำดับ:
9, 3, 1, 6, 4, 7, 10, 14, 13
ผลลัพธ์
Pre-order traversal: 9, 3, 1, 6, 4, 7, 10, 14, 13
ตรวจสอบตัวเลือก
- a) 1, 3, 4, 6, 7, 9, 10, 13, 14
 (นี่คือ In-order)
(นี่คือ In-order) - b) 1, 4, 7, 6, 3, 13, 14, 10, 9
 (นี่คือ Post-order)
(นี่คือ Post-order) - c) 9, 3, 1, 6, 4, 7, 10, 14, 13
 (Pre-order)
(Pre-order) - d) 9, 3, 10, 1, 6, 14, 4, 7, 13
 (ผิดลำดับ)
(ผิดลำดับ)
คำตอบ: c) 9, 3, 1, 6, 4, 7, 10, 14, 13 
เปรียบเทียบ 3 แบบการเดินผ่าน
| แบบ | ลำดับ | ผลลัพธ์ |
|---|---|---|
| Pre-order | Root → Left → Right | 9, 3, 1, 6, 4, 7, 10, 14, 13 |
| In-order | Left → Root → Right | 1, 3, 4, 6, 7, 9, 10, 13, 14 |
| Post-order | Left → Right → Root | 1, 4, 7, 6, 3, 13, 14, 10, 9 |
คำตอบและวิธีทำ
หลักการ Queue (คิว)
Queue เป็นโครงสร้างข้อมูลแบบ FIFO (First In First Out) = เข้าก่อนออกก่อน
- ENQ n : เพิ่มข้อมูล n เข้าไปในคิว (Enqueue)
- DEQ : นำข้อมูลออกจากคิว (Dequeue) - เอาตัวที่เข้าก่อนออกก่อน
ติดตามการดำเนินการทีละขั้นตอน
ลำดับ: ENQ 1, ENQ 2, ENQ 3, DEQ, ENQ 4, ENQ 5, DEQ, ENQ 6, DEQ, DEQ
| ขั้นตอน | คำสั่ง | สถานะคิว | หมายเหตุ |
|---|---|---|---|
| เริ่มต้น | - | คิวว่าง | |
| 1 | ENQ 1 | [1] | เพิ่ม 1 |
| 2 | ENQ 2 | [1, 2] | เพิ่ม 2 |
| 3 | ENQ 3 | [1, 2, 3] | เพิ่ม 3 |
| 4 | DEQ | [2, 3] | นำ 1 ออก |
| 5 | ENQ 4 | [2, 3, 4] | เพิ่ม 4 |
| 6 | ENQ 5 | [2, 3, 4, 5] | เพิ่ม 5 |
| 7 | DEQ | [3, 4, 5] | นำ 2 ออก |
| 8 | ENQ 6 | [3, 4, 5, 6] | เพิ่ม 6 |
| 9 | DEQ | [4, 5, 6] | นำ 3 ออก |
| 10 | DEQ | [5, 6] | นำ 4 ออก |
หลังดำเนินการครบทุกคำสั่งแล้ว
คิวมีข้อมูล: [5, 6]
- ตัวหน้าสุด (Front): 5
- ตัวท้ายสุด (Rear): 6
โจทย์ถามว่า
“ข้อใดคือค่าที่จะถูกนำออกมา” (หากทำ DEQ อีกครั้ง)
เมื่อทำ DEQ อีกครั้ง (ครั้งที่ 5):
- จะนำตัวที่อยู่หน้าสุดออก
- คือ 5
ภาพประกอบ
Front → [5, 6] ← Rear
↑
DEQ ครั้งต่อไป
จะนำ 5 ออก
คำตอบ: c) 5 
สรุปหลักการ
Queue:
- เข้าจากด้านหลัง (Rear)
- ออกจากด้านหน้า (Front)
- FIFO: First In First Out
ในตัวอย่างนี้:
- ตัวเลขที่เข้าคิวลำดับสุดท้าย: 5, 6
- ตัวเลขที่จะออกก่อน: 5 (เข้าก่อน 6)
เทคนิคหาคำตอบแบบรวดเร็ว 
 เทคนิค 1: นับจำนวน ENQ และ DEQ
เทคนิค 1: นับจำนวน ENQ และ DEQ
หลักการ: Queue คงเหลือ = จำนวน ENQ - จำนวน DEQ
ลำดับ: ENQ 1, ENQ 2, ENQ 3, DEQ, ENQ 4, ENQ 5, DEQ, ENQ 6, DEQ, DEQ
✓ นับ ENQ: 1, 2, 3, 4, 5, 6 → 6 ครั้ง
✓ นับ DEQ: (4 ครั้ง)
✓ เหลือในคิว = 6 - 4 = 2 ตัว
สรุป:
- เหลือ 2 ตัวสุดท้าย ที่ ENQ เข้าไป = 5 และ 6
- ตัวที่จะออกก่อน = 5 (เข้าก่อน)
![]() ประหยัดเวลา: ~70%
ประหยัดเวลา: ~70%
 เทคนิค 2: ติดตามเฉพาะจุดสำคัญ
เทคนิค 2: ติดตามเฉพาะจุดสำคัญ
หลักการ: ดูเฉพาะตำแหน่ง DEQ ว่าเอาอะไรออก
ENQ 1, ENQ 2, ENQ 3, ❌DEQ → นำ 1 ออก
มีอยู่: [2, 3]
ENQ 4, ENQ 5, ❌DEQ → นำ 2 ออก
มีอยู่: [3, 4, 5]
ENQ 6, ❌DEQ, ❌DEQ → นำ 3 และ 4 ออก
เหลือ: [5, 6]
ตัวหน้าคิว (จะออกต่อไป): 5
![]() ประหยัดเวลา: ~60%
ประหยัดเวลา: ~60%
 เทคนิค 3: วิเคราะห์ลำดับเข้า-ออก (เร็วสุด!)
เทคนิค 3: วิเคราะห์ลำดับเข้า-ออก (เร็วสุด!)
ขั้นตอน:
 เขียนลำดับที่เข้าทั้งหมด
เขียนลำดับที่เข้าทั้งหมด
เข้า: 1 → 2 → 3 → 4 → 5 → 6
 นับว่า DEQ กี่ครั้ง
นับว่า DEQ กี่ครั้ง
DEQ จำนวน: 4 ครั้ง
 ขีดเส้นตัดตัวแรก 4 ตัว
ขีดเส้นตัดตัวแรก 4 ตัว
เข้า: 1̶ → 2̶ → 3̶ → 4̶ → 5 → 6
↑___ออกไปแล้ว___↑ ↑__เหลืออยู่__↑
 ตัวที่เหลือและตัวหน้าสุด
ตัวที่เหลือและตัวหน้าสุด
เหลือ: [5, 6]
หน้าสุด: 5 ← จะออกในครั้งต่อไป
![]() ประหยัดเวลา: ~80%
ประหยัดเวลา: ~80%
 เทคนิค 4: สูตรคำนวณตำแหน่ง (สำหรับโจทย์ที่ซับซ้อน)
เทคนิค 4: สูตรคำนวณตำแหน่ง (สำหรับโจทย์ที่ซับซ้อน)
ตำแหน่งหน้าคิว = (จำนวน DEQ) + 1
= 4 + 1
= 5 ← ตัวเลขลำดับที่ 5 ที่เข้าคิว
จากลำดับที่เข้า: 1, 2, 3, 4, 5, 6
คำตอบ: 5 ![]()
 เปรียบเทียบเทคนิค
เปรียบเทียบเทคนิค
| เทคนิค | เวลา | ความแม่นยำ | เหมาะกับ |
|---|---|---|---|
| วิธีปกติ (ติดตามทุกขั้น) | 100% | 100% | ผู้เริ่มต้น |
| เทคนิค 1: นับ ENQ/DEQ | 30% | 95% | โจทย์ทั่วไป |
| เทคนิค 2: ดูจุดสำคัญ | 40% | 90% | ควบคุมความผิดพลาด |
| เทคนิค 3: ขีดเส้นตัด | 20% | 100% | แนะนำสำหรับสอบ |
| เทคนิค 4: สูตร | 10% | 100% | เร็วสุด! |
 เคล็ดลับการใช้งาน
เคล็ดลับการใช้งาน
 ใช้เทคนิค 3 หรือ 4 เมื่อ:
ใช้เทคนิค 3 หรือ 4 เมื่อ:
- โจทย์มี ENQ/DEQ เยอะมาก
- ต้องการความเร็ว
- มั่นใจในการนับ
 ใช้เทคนิค 1 หรือ 2 เมื่อ:
ใช้เทคนิค 1 หรือ 2 เมื่อ:
- ต้องการความแม่นยำสูง
- โจทย์ซับซ้อน (มีเงื่อนไขพิเศษ)
- ต้องการเช็คคำตอบ
 ข้อควรระวัง:
ข้อควรระวัง:
- ต้องนับจำนวน ENQ และ DEQ ให้ถูก
- อย่าลืมว่า Queue เป็น FIFO
- ตรวจสอบว่าโจทย์ถามตัวหน้าหรือตัวท้าย
 ตัวอย่างใช้เทคนิค 4 แบบรวดเร็ว
ตัวอย่างใช้เทคนิค 4 แบบรวดเร็ว
โจทย์เดิม:
ENQ 1, ENQ 2, ENQ 3, DEQ, ENQ 4, ENQ 5, DEQ, ENQ 6, DEQ, DEQ
แก้แบบไว:
1. เขียนลำดับที่เข้า: 1, 2, 3, 4, 5, 6
2. นับ DEQ: 4 ครั้ง
3. ตำแหน่งหน้าคิว = 4 + 1 = 5
4. ลำดับที่ 5 = เลข 5
คำตอบ: 5 ![]()
เวลาใช้: ~10 วินาที ![]()
 สรุป
สรุป
| เมื่อไหร่ | ใช้เทคนิคไหน |
|---|---|
| สอบจริง (เวลาน้อย) | เทคนิค 3 หรือ 4 |
| ฝึกทำโจทย์ | เทคนิค 1 หรือ 2 |
| เช็คคำตอบ | วิธีปกติ (ติดตามทุกขั้น) |
หัวใจสำคัญ:
- Queue = FIFO (เข้าก่อนออกก่อน)
- นับ DEQ แล้วบวก 1 = ตำแหน่งหน้าคิว
- ขีดเส้นตัดตัวที่ออกไปแล้ว = เหลือตัวไหน
คำตอบข้อนี้: c) 5 ![]()
คำตอบและวิธีทำ
วิเคราะห์โจทย์
Hashing Function: mod(a₁+a₂+a₃+a₄+a₅, 13)
- ข้อมูล: 54321
- Hash Table Size: 13 ตำแหน่ง (0-12)
- วิธีการ: บวกตัวเลขทุกหลักแล้วหาร mod 13
วิธีแก้แบบปกติ
ขั้นที่ 1: แยกตัวเลขแต่ละหลัก
54321 แยกเป็น:
a₁ = 5
a₂ = 4
a₃ = 3
a₄ = 2
a₅ = 1
ขั้นที่ 2: คำนวณผลรวม
a₁ + a₂ + a₃ + a₄ + a₅
= 5 + 4 + 3 + 2 + 1
= 15
ขั้นที่ 3: หา mod 13
mod(15, 13) = 15 % 13 = ?
15 ÷ 13 = 1 เศษ 2
ผลลัพธ์: 15 mod 13 = 2
ดังนั้น เก็บข้อมูลที่ตำแหน่ง 2
 เทคนิคหาคำตอบแบบรวดเร็ว
เทคนิคหาคำตอบแบบรวดเร็ว
เทคนิค 1: ใช้สูตรรวดเร็ว 
สำหรับเลขที่เรียงกัน (เช่น 54321, 12345):
ผลรวม = n × (first + last) / 2
โดยที่:
- n = จำนวนตัวเลข
- first = ตัวแรก
- last = ตัวสุดท้าย
ตัวอย่างนี้:
54321 → เลขเรียงจาก 5 ลงมา 1
n = 5 ตัว
first = 5, last = 1
ผลรวม = 5 × (5 + 1) / 2
= 5 × 6 / 2
= 30 / 2
= 15
15 mod 13 = 2
![]() ประหยัดเวลา: ~40%
ประหยัดเวลา: ~40%
เทคนิค 2: จำหลัก mod ที่ใช้บ่อย 
ตาราง mod 13 ที่ใช้บ่อย:
| ผลรวม | mod 13 | ผลรวม | mod 13 |
|---|---|---|---|
| 0 | 0 | 13 | 0 |
| 1 | 1 | 14 | 1 |
| 2 | 2 | 15 | 2 ← |
| 3 | 3 | 16 | 3 |
| 4 | 4 | 17 | 4 |
| 5 | 5 | 18 | 5 |
| 6 | 6 | 19 | 6 |
| 7 | 7 | 20 | 7 |
| 8 | 8 | 21 | 8 |
| 9 | 9 | 22 | 9 |
| 10 | 10 | 23 | 10 |
| 11 | 11 | 24 | 11 |
| 12 | 12 | 25 | 12 |
เทคนิคจำ:
- ถ้าผลรวม < 13 → mod = ตัวเอง
- ถ้าผลรวม ≥ 13 → ลบ 13 ไปเรื่อยๆ จนเหลือ < 13
ตัวอย่าง:
15 - 13 = 2
![]() ประหยัดเวลา: ~30%
ประหยัดเวลา: ~30%
เทคนิค 3: คำนวณในใจแบบเร็ว 

วิธีคิดในหัว:
5 + 4 = 9
9 + 3 = 12
12 + 2 = 14
14 + 1 = 15
15 เทียบกับ 13:
15 - 13 = 2
หรือแบบ “บวกเลื่อน”:
5+4=9, +3=12, +2=14, +1=15
15-13=2
![]() ประหยัดเวลา: ~50%
ประหยัดเวลา: ~50%
เทคนิค 4: ใช้สมบัติของ mod (สำหรับผู้เชี่ยวชาญ) 
สูตร: (a + b) mod n = [(a mod n) + (b mod n)] mod n
(5+4+3+2+1) mod 13
= [(5 mod 13) + (4 mod 13) + (3 mod 13) + (2 mod 13) + (1 mod 13)] mod 13
= [5 + 4 + 3 + 2 + 1] mod 13
= 15 mod 13
= 2
หรือแบบทีละขั้น:
5 mod 13 = 5
(5 + 4) mod 13 = 9 mod 13 = 9
(9 + 3) mod 13 = 12 mod 13 = 12
(12 + 2) mod 13 = 14 mod 13 = 1 ← ลบ 13 ได้ 1
(1 + 1) mod 13 = 2 mod 13 = 2
![]() ประหยัดเวลา: ~20% (แต่ป้องกัน overflow ในเลขใหญ่)
ประหยัดเวลา: ~20% (แต่ป้องกัน overflow ในเลขใหญ่)
 สรุปเปรียบเทียบเทคนิค
สรุปเปรียบเทียบเทคนิค
| เทคนิค | เวลา | ความยาก | เหมาะกับ |
|---|---|---|---|
| วิธีปกติ | 100% | ผู้เริ่มต้น | |
| สูตรรวดเร็ว | 60% | เลขเรียงลำดับ |
|
| จำตาราง mod | 70% | สอบจริง | |
| คิดในหัว | 50% | ฝึกฝนแล้ว |
|
| สมบัติ mod | 80% | เลขใหญ่มาก |
 เคล็ดลับการจำ mod
เคล็ดลับการจำ mod
วิธีหา x mod 13 แบบเร็ว:
ถ้า x < 13 → mod = x
ถ้า x ≥ 13 → ลบ 13 ทีละครั้ง
ตัวอย่าง:
27 mod 13 = 27 - 13 = 14 - 13 = 1
40 mod 13 = 40 - 13 = 27 - 13 = 14 - 13 = 1
วิธีการคำนวณ mod แบบหาร:
x mod 13 = x - (13 × ⌊x/13⌋)
15 mod 13 = 15 - (13 × ⌊15/13⌋)
= 15 - (13 × 1)
= 15 - 13
= 2
 ตัวอย่างเพิ่มเติม
ตัวอย่างเพิ่มเติม
ถ้าเลขเป็น 98765:
วิธีเร็ว:
ผลรวม = 9+8+7+6+5 = 35
35 mod 13 = 35 - 13 = 22 - 13 = 9
ตำแหน่ง: 9
ถ้าเลขเป็น 11111:
วิธีเร็ว:
ผลรวม = 1+1+1+1+1 = 5
5 mod 13 = 5
ตำแหน่ง: 5
 ข้อควรระวัง
ข้อควรระวัง
-
อย่าลืมว่า mod ให้ผลลัพธ์ 0 ถึง (n-1)
- mod 13 ได้ 0-12 เท่านั้น
-
ตรวจสอบว่าโจทย์ใช้ mod หรือ remainder
- ส่วนใหญ่เหมือนกัน แต่อาจต่างในกรณีเลขลบ
-
ระวังเลขใหญ่
- ใช้เทคนิคสมบัติ mod ถ้าเลขใหญ่มาก
คำตอบ: b) 2 
แสดงในตาราง:
ตำแหน่ง อาร์เรย์
0 [ ]
1 [ ]
2 [54321] ← เก็บที่นี่
3 [ ]
: :
11 [ ]
12 [ ]
สรุป: ใช้เทคนิคไหนก็ได้ตามความถนัด แต่แนะนำ “บวกแล้วลบ 13” สำหรับสอบจริง เพราะเร็วและแม่นยำ!
คำตอบและวิธีทำ
วิเคราะห์โจทย์
โจทย์ถามเทคโนโลยีที่:
- ประมวลผลแบบโต้ตอบ (Interactive processing)
- ทำงานอยู่เฉพาะบนเว็บเซิร์ฟเวอร์เท่านั้น (Server-side only)
วิเคราะห์แต่ละตัวเลือก
a) JavaScript 
ที่ทำงาน: Client-side (ในเบราว์เซอร์)
[เบราว์เซอร์] ← JavaScript ทำงานที่นี่
↕
[เว็บเซิร์ฟเวอร์]
คุณสมบัติ:
 โต้ตอบกับผู้ใช้ได้
โต้ตอบกับผู้ใช้ได้ ทำงานบน client-side ไม่ใช่เซิร์ฟเวอร์
ทำงานบน client-side ไม่ใช่เซิร์ฟเวอร์- ใช้สำหรับ: Animation, Form validation, DOM manipulation
สรุป: ไม่ใช่คำตอบ เพราะทำงานบน client
b) Java Applet 
ที่ทำงาน: Client-side (ดาวน์โหลดมารันในเบราว์เซอร์)
[เว็บเซิร์ฟเวอร์] → ส่ง Applet (.class)
↓
[เบราว์เซอร์] ← Applet ทำงานที่นี่ (ใน JVM)
คุณสมบัติ:
 โต้ตอบกับผู้ใช้ได้
โต้ตอบกับผู้ใช้ได้ ทำงานบน client-side ไม่ใช่เซิร์ฟเวอร์
ทำงานบน client-side ไม่ใช่เซิร์ฟเวอร์- ดาวน์โหลดจากเซิร์ฟเวอร์แล้วรันบนเครื่อง client
- หมายเหตุ: เลิกใช้แล้วตั้งแต่ปี 2017
สรุป: ไม่ใช่คำตอบ เพราะทำงานบน client
c) Java Servlet 
ที่ทำงาน: Server-side เท่านั้น
[เบราว์เซอร์] → ส่ง HTTP Request
↓
[เว็บเซิร์ฟเวอร์]
↓
[Servlet Container] ← Servlet ทำงานที่นี่
↓
[Database/Resources]
คุณสมบัติ:
 โต้ตอบกับผู้ใช้ได้ (รับ request/ส่ง response)
โต้ตอบกับผู้ใช้ได้ (รับ request/ส่ง response) ทำงานบน server-side เท่านั้น
ทำงานบน server-side เท่านั้น- ประมวลผลบนเซิร์ฟเวอร์
- ส่งผลลัพธ์กลับไปที่ client
ตัวอย่างการทำงาน:
java
public class HelloServlet extends HttpServlet {
protected void doGet(HttpServletRequest request,
HttpServletResponse response) {
// ประมวลผลบนเซิร์ฟเวอร์
String name = request.getParameter("name");
response.getWriter().println("Hello " + name);
}
}
สรุป: นี่คือคำตอบ! ![]()
d) VBScript 
ที่ทำงาน: ส่วนใหญ่ Client-side (IE เท่านั้น)
[เบราว์เซอร์ IE] ← VBScript ทำงานที่นี่ (client-side)
หรือ
[เซิร์ฟเวอร์ IIS] ← ASP + VBScript (server-side)
คุณสมบัติ:
 โต้ตอบกับผู้ใช้ได้
โต้ตอบกับผู้ใช้ได้ ทำงานได้ทั้ง client-side และ server-side
ทำงานได้ทั้ง client-side และ server-side- ใช้ได้เฉพาะ Internet Explorer
- เลิกใช้แล้ว (deprecated)
สรุป: ไม่ใช่คำตอบ เพราะไม่ได้ทำงานเฉพาะบนเซิร์ฟเวอร์เท่านั้น
 ตารางเปรียบเทียบ
ตารางเปรียบเทียบ
| เทคโนโลยี | ทำงานที่ | โต้ตอบได้ | เฉพาะเซิร์ฟเวอร์ | สถานะ |
|---|---|---|---|---|
| JavaScript | Client | ใช้งานอยู่ | ||
| Java Applet | Client | เลิกใช้แล้ว | ||
| Java Servlet | Server | ใช้งานอยู่ |
||
| VBScript | Client/Server | เลิกใช้แล้ว |
 เทคนิคจำง่ายๆ
เทคนิคจำง่ายๆ
จำคำว่า “Servlet”
Servlet = Server + let (ขนาดเล็ก)
= โปรแกรมเล็กๆ ที่ทำงานบน Server
จำความแตกต่าง
Client-side (รันในเบราว์เซอร์):
├─ JavaScript ⭐ (ใช้มาก)
├─ Java Applet (เลิกใช้)
└─ VBScript (เลิกใช้)
Server-side (รันบนเซิร์ฟเวอร์):
├─ Java Servlet ⭐ (คำตอบ)
├─ PHP
├─ Python (Django/Flask)
├─ Node.js
└─ ASP.NET
 ข้อมูลเพิ่มเติม
ข้อมูลเพิ่มเติม
Java Servlet คืออะไร?
นิยาม:
- คลาส Java ที่ทำงานบนเว็บเซิร์ฟเวอร์
- ขยายความสามารถของเซิร์ฟเวอร์
- จัดการ HTTP request/response
ข้อดี:
 ประสิทธิภาพสูง (compile แล้ว)
ประสิทธิภาพสูง (compile แล้ว) ปลอดภัย (ทำงานบนเซิร์ฟเวอร์)
ปลอดภัย (ทำงานบนเซิร์ฟเวอร์) มีฟีเจอร์ครบ (session, cookie, etc.)
มีฟีเจอร์ครบ (session, cookie, etc.) Platform independent
Platform independent
ใช้งานจริง:
- Web applications
- RESTful APIs
- Backend processing
- Database connectivity
 เทคนิคจำแบบเร็ว
เทคนิคจำแบบเร็ว
คำถาม: ทำงานบนเซิร์ฟเวอร์เท่านั้น?
❓ JavaScript? → ❌ Client
❓ Applet? → ❌ Client
❓ Servlet? → ✅ Server ← คำตอบ!
❓ VBScript? → ❌ Client/Server
สูตรจำ:
"Let" = เล็ก
Servlet = Server + let = ตัวเล็กๆ ที่ทำงานบน Server
App + let = แอพเล็กๆ ที่ทำงานบน Client
คำตอบ: c) จาวาเซิร์ฟเล็ต (Java servlet) 
เหตุผล:
 ทำงานเฉพาะบนเว็บเซิร์ฟเวอร์
ทำงานเฉพาะบนเว็บเซิร์ฟเวอร์ ประมวลผลแบบโต้ตอบกับ client ได้
ประมวลผลแบบโต้ตอบกับ client ได้ รับ request จาก client → ประมวลผล → ส่ง response กลับ
รับ request จาก client → ประมวลผล → ส่ง response กลับ ยังใช้งานอยู่ในปัจจุบัน
ยังใช้งานอยู่ในปัจจุบัน
ตัวเลือกอื่นผิดเพราะ:
- a) JavaScript → ทำงานบน client
- b) Java Applet → ทำงานบน client
- d) VBScript → ทำงานได้ทั้ง client และ server (ไม่ใช่เฉพาะเซิร์ฟเวอร์)
คำตอบและวิธีทำ
วิเคราะห์โจทย์
โจทย์ถามเกี่ยวกับ Special Register ที่ใช้ในการ:
- Push (เพิ่มข้อมูลเข้า stack)
- Pop (นำข้อมูลออกจาก stack)
วิเคราะห์แต่ละตัวเลือก
a) รีจิสเตอร์คำสั่ง (Instruction Register - IR) 
หน้าที่:
- เก็บ คำสั่งปัจจุบัน ที่กำลังถูก execute
- ใช้ในขั้นตอน Fetch-Decode-Execute
[Memory] → Fetch → [IR] → Decode → Execute
ตัวอย่าง:
IR = ADD R1, R2 ← เก็บคำสั่ง ADD
สรุป: ไม่เกี่ยวกับ Stack, Push, Pop
b) ตัวนับโปรแกรม (Program Counter - PC) 
หน้าที่:
- เก็บ address ของคำสั่งถัดไป ที่จะ execute
- เพิ่มค่าทีละ 1 (หรือมากกว่า) หลัง fetch คำสั่ง
PC = 1000 → Fetch instruction at 1000
PC = 1001 → Fetch instruction at 1001
PC = 1002 → ...
ตัวอย่าง:
Address | Instruction
--------|------------
1000 | MOV R1, #5
1001 | ADD R2, R1 ← PC ชี้ที่นี่
1002 | SUB R3, R2
สรุป: ไม่เกี่ยวกับ Stack, Push, Pop
c) ตัวชี้สแตก (Stack Pointer - SP) 
หน้าที่:
- ชี้ไปที่ top ของ stack (ตำแหน่งล่าสุด)
- ใช้ใน PUSH operation
- ใช้ใน POP operation
- อัพเดทค่าอัตโนมัติ เมื่อมีการ push/pop
การทำงาน:
Stack (เติบโตลงล่าง):
High Address
↓
[ ]
[ ]
[ 30 ] ← SP (ชี้ที่นี่)
[ 20 ]
[ 10 ]
Low Address
PUSH Operation:
PUSH 40
ขั้นตอน:
1. SP = SP - 1 (เลื่อน SP ลง)
2. Memory[SP] = 40 (เก็บข้อมูล)
ผลลัพธ์:
[ 40 ] ← SP (ชี้ใหม่)
[ 30 ]
[ 20 ]
[ 10 ]
POP Operation:
POP
ขั้นตอน:
1. Data = Memory[SP] (อ่านข้อมูล)
2. SP = SP + 1 (เลื่อน SP ขึ้น)
ผลลัพธ์:
[ ]
[ 30 ] ← SP (ชี้ใหม่)
[ 20 ]
[ 10 ]
สรุป: นี่คือคำตอบ! ใช้ในการ Push และ Pop ![]()
d) รีจิสเตอร์สถานะ (Status Register / Flags Register) 
หน้าที่:
- เก็บ สถานะ หรือ flags ต่างๆ ของ CPU
- แต่ละบิตมีความหมายต่างกัน
Flags ที่มีโดยทั่วไป:
Bit: 7 6 5 4 3 2 1 0
[S][Z][--][AC][--][P][--][C]
C = Carry Flag
P = Parity Flag
AC = Auxiliary Carry Flag
Z = Zero Flag
S = Sign Flag
ตัวอย่างการใช้งาน:
SUB A, B
ถ้า A = B:
Zero Flag (Z) = 1 ← ผลลัพธ์เป็น 0
ถ้า A < B:
Carry Flag (C) = 1 ← เกิด borrow
Sign Flag (S) = 1 ← ผลลัพธ์ติดลบ
สรุป: ไม่เกี่ยวกับ Stack, Push, Pop
 ตารางเปรียบเทียบ
ตารางเปรียบเทียบ
| Register | หน้าที่หลัก | ใช้กับ Stack? | ใช้กับ Push/Pop? |
|---|---|---|---|
| Instruction Register (IR) | เก็บคำสั่งปัจจุบัน | ||
| Program Counter (PC) | ชี้คำสั่งถัดไป | ||
| Stack Pointer (SP) | ชี้ top ของ stack | ||
| Status Register (SR) | เก็บ flags สถานะ |
 ทำความเข้าใจ Stack Pointer
ทำความเข้าใจ Stack Pointer
โครงสร้าง Stack
Stack มี 2 แบบ:
1. Full Descending (ใช้มาก):
- SP ชี้ที่ occupied location
- เติบโตจากบนลงล่าง
- PUSH: SP--, then store
- POP: load, then SP++
2. Empty Ascending:
- SP ชี้ที่ empty location
- เติบโตจากล่างขึ้นบน
- PUSH: store, then SP++
- POP: SP--, then load
ตัวอย่างโค้ด Assembly
assembly
; PUSH operation
PUSH AX ; Push AX register to stack
; CPU ทำเบื้องหลัง:
; SP = SP - 2 (สมมุติ 16-bit)
; [SP] = AX
; POP operation
POP BX ; Pop from stack to BX
; CPU ทำเบื้องหลัง:
; BX = [SP]
; SP = SP + 2
 เทคนิคจำง่ายๆ
เทคนิคจำง่ายๆ
จำคำว่า “Pointer”
Stack POINTER = ตัวชี้ Stack
= ชี้ไปที่ตำแหน่งบน Stack
= ใช้กับ Push/Pop
จำความสัมพันธ์
Stack ←→ Stack Pointer ←→ Push/Pop
เหมือน:
ถังน้ำ ←→ ไม้บรรทัดวัดระดับ ←→ เติม/ตัก
เปรียบเทียบกับของจริง
Stack of plates (จานซ้อน):
[จาน 3] ← SP ชี้ที่นี่ (จานบนสุด)
[จาน 2]
[จาน 1]
---------
PUSH จาน 4:
[จาน 4] ← SP เลื่อนมาชี้ที่นี่
[จาน 3]
[จาน 2]
[จาน 1]
POP:
(เอาจาน 4 ออก)
[จาน 3] ← SP กลับมาชี้ที่นี่
[จาน 2]
[จาน 1]
 เทคนิคจำแบบรวดเร็ว
เทคนิคจำแบบรวดเร็ว
คำถาม: ใช้กับ Push/Pop?
❓ IR (คำสั่ง)? → ❌ เก็บคำสั่ง
❓ PC (นับโปรแกรม)? → ❌ ชี้คำสั่งถัดไป
❓ SP (ชี้ Stack)? → ✅ ใช้ Push/Pop ← คำตอบ!
❓ SR (สถานะ)? → ❌ เก็บ flags
สูตรจำ:
Stack + Pointer = Stack Pointer
= ใช้กับ Stack
= ใช้กับ Push/Pop
คำตอบ: c) ตัวชี้สแตก (Stack pointer) 
เหตุผล:
 Stack Pointer ชี้ไปที่ top ของ stack
Stack Pointer ชี้ไปที่ top ของ stack ใช้ใน PUSH operation (เพิ่มข้อมูลลง stack)
ใช้ใน PUSH operation (เพิ่มข้อมูลลง stack) ใช้ใน POP operation (เอาข้อมูลออกจาก stack)
ใช้ใน POP operation (เอาข้อมูลออกจาก stack) อัพเดทค่าอัตโนมัติ ทุกครั้งที่ push/pop
อัพเดทค่าอัตโนมัติ ทุกครั้งที่ push/pop
ตัวเลือกอื่นผิดเพราะ:
- a) Instruction Register → เก็บคำสั่งที่กำลัง execute
- b) Program Counter → ชี้ address ของคำสั่งถัดไป
- d) Status Register → เก็บ flags สถานะต่างๆ
 สรุปหลักการ
สรุปหลักการ
Stack Pointer คือ:
- รีจิสเตอร์พิเศษที่จำเป็นสำหรับการทำงานของ Stack
- ใช้ในการเรียก function (function call)
- ใช้ในการเก็บ return address
- ใช้ในการเก็บตัวแปร local
- หัวใจสำคัญของ Push และ Pop operations!
คำตอบที่ถูกต้องคือ b) การขัดจังหวะที่เกิดจากการดำเนินการคำสั่งที่มีการหารด้วยศูนย์ (\text{divide-by-zero operation})
การวิเคราะห์และการจัดประเภท \text{Interrupt}
การขัดจังหวะ (\text{Interrupt}) แบ่งออกเป็น 2 ประเภทหลักๆ ตามแหล่งที่มา:
-
\text{External Interrupt} (การขัดจังหวะภายนอก):
- เกิดจากอุปกรณ์ภายนอก (\text{I/O device}) หรือสัญญาณจากภายนอก \text{CPU}
- เช่น การกดแป้นพิมพ์, การขัดจังหวะเมื่อ \text{I/O} ทำงานเสร็จ, หรือไฟฟ้าดับ
-
\text{Internal Interrupt} หรือ \text{Trap/Exception} (การขัดจังหวะภายใน):
- เกิดจากความผิดพลาดขณะที่ \text{CPU} กำลังดำเนินการคำสั่ง (\text{executing an instruction})
- เป็นสิ่งที่ผิดปกติที่เกิดขึ้นภายในตัวโปรแกรมเอง
- เช่น การหารด้วยศูนย์, การเข้าถึงหน่วยความจำที่ผิดกฎหมาย (\text{illegal memory access}), หรือการใช้คำสั่งที่ไม่ถูกต้อง (\text{illegal instruction}
- มักถูกเรียกว่า \text{Exception} หรือ \text{Trap}
การวิเคราะห์ตัวเลือก
| ตัวเลือก | เหตุการณ์ | แหล่งที่มา/ประเภท | เหตุผล |
|---|---|---|---|
| a) การจ่ายไฟผิดปกติ | ไฟฟ้าดับไปชั่วขณะ | \text{External} (เกิดจากแหล่งจ่ายไฟภายนอกระบบหลักของ \text{CPU}) | |
| b) การหารด้วยศูนย์ (\text{divide-by-zero}) | เกิดจากการดำเนินการคำสั่งที่ผิดพลาด | \text{Internal} (\text{Exception}/\text{Trap}) | เป็นความผิดพลาดที่ \text{CPU} ตรวจพบขณะรันคำสั่งนั้นๆ |
| c) การเสร็จสิ้นการทำงานของ \text{Input/Output} | \text{I/O device} ส่งสัญญาณเสร็จสิ้นมา | \text{External} (เกิดจากอุปกรณ์ \text{I/O} ภายนอก \text{CPU}) | |
| d) ความผิดพลาดของพาริตีหน่วยความจำ (\text{memory parity error}) | เกิดจากความผิดพลาดในการส่งข้อมูลของ \text{Memory} | \text{External} (เกิดจาก \text{Memory} ซึ่งเป็นส่วนประกอบภายนอก \text{CPU}) |
ดังนั้น b) คือเหตุการณ์เดียวที่เกิดจากความผิดปกติใน การดำเนินการของคำสั่ง ซึ่งจัดเป็น \text{Internal Interrupt} หรือ \text{Exception}
คำตอบที่ถูกต้องคือ b) การเขียนทีหลัง (\text{Write back})
เทคนิคการจัดการการเขียนข้อมูล (\text{Cache Write Policies})
คำถามนี้เกี่ยวข้องกับ นโยบายการเขียนข้อมูล (\text{Write Policy}) ในหน่วยความจำแคช (\text{Cache Memory}) ซึ่งเป็นเทคนิคที่ใช้ในการจัดการว่าเมื่อ \text{CPU} มีการแก้ไขข้อมูลใน \text{Cache} จะต้องอัปเดตข้อมูลใน หน่วยความจำหลัก (\text{Main Memory}) เมื่อใด
| นโยบายการเขียน | คำอธิบาย | จุดเด่น/จุดประสงค์ |
|---|---|---|
| b) การเขียนทีหลัง (\text{Write back}) | \text{CPU} จะทำการอัปเดตข้อมูล เฉพาะใน \text{Cache} เท่านั้น โดยจะทำเครื่องหมาย (\text{flag}) ว่า \text{Block} นั้นเป็นข้อมูลใหม่ (\text{Dirty}) และจะรออัปเดตข้อมูลไปยังหน่วยความจำหลัก ในภายหลัง (เมื่อ \text{Block} นั้นถูกนำออก/ถูกแทนที่จาก \text{Cache}) | ลดจำนวนครั้ง ของการเขียนข้อมูลไปยังหน่วยความจำหลัก ซึ่งช่วยเพิ่มประสิทธิภาพความเร็วในการทำงานของ \text{CPU} ได้มากที่สุด |
| d) การเขียนทั้งหมด (\text{Write through}) | \text{CPU} จะทำการอัปเดตข้อมูล ทั้งใน \text{Cache} และหน่วยความจำหลักพร้อมกัน ในทันทีที่เกิดการเขียน | ข้อมูลใน \text{Cache} และ \text{Main Memory} จะมีความสอดคล้องกัน (\text{Consistency}) อยู่ตลอดเวลา แต่จะเกิดการ \text{Write} ไปยัง \text{Main Memory} บ่อยครั้ง ทำให้ช้าลง |
สรุปเหตุผล
โจทย์ต้องการเทคนิคที่ “ลดจำนวนครั้งของกระบวนการเขียนข้อมูลที่กระทำต่อหน่วยความจำหลัก” โดยการอัปเดตเฉพาะใน \text{Cache} ก่อน แล้วจึงอัปเดตทีหลัง ซึ่งตรงกับหลักการของ การเขียนทีหลัง (\text{Write back}) โดยสมบูรณ์
- a) \text{การซ้อนแทน} (\text{Overlay}) : เป็นเทคนิคการจัดการหน่วยความจำที่อนุญาตให้โปรแกรมขนาดใหญ่ทำงานในหน่วยความจำที่มีจำกัด (ไม่เกี่ยวกับ \text{Write Policy} ของ \text{Cache})
- c) \text{การป้องกันการเขียน} (\text{Write protected}) : เป็นการตั้งค่าเพื่อไม่ให้สามารถแก้ไขข้อมูลได้ (ไม่ใช่นโยบายการเขียน)
คำตอบ: c) สร้างวัตถุสามมิติต่าง ๆ ขึ้นมาด้วยวิธีการต่าง ๆ เช่นการขึ้นรูปด้วยภาพลอมฟิลาเมนต์ 
เหตุผล:
 อธิบายหน้าที่หลักของเครื่องพิมพ์ 3D ได้ถูกต้อง
อธิบายหน้าที่หลักของเครื่องพิมพ์ 3D ได้ถูกต้อง ยกตัวอย่าง FDM/FFF ซึ่งเป็นเทคโนโลยีที่ใช้กันมากที่สุด
ยกตัวอย่าง FDM/FFF ซึ่งเป็นเทคโนโลยีที่ใช้กันมากที่สุด “การขึ้นรูปด้วยภาพลอมฟิลาเมนต์” = Fused Filament Fabrication
“การขึ้นรูปด้วยภาพลอมฟิลาเมนต์” = Fused Filament Fabrication สร้างวัตถุ 3D จริง จากไฟล์ดิจิทัล
สร้างวัตถุ 3D จริง จากไฟล์ดิจิทัล
ตัวเลือกอื่นผิดเพราะ:
- a) 3D Scanning (input) ไม่ใช่ 3D Printing (output)
- b) Thermal Printing 2D ไม่ใช่ 3D
- d) Texture Mapping (CG) ไม่ใช่การสร้างวัตถุจริง
 ความรู้เพิ่มเติม
ความรู้เพิ่มเติม
ประเภทของ 3D Printing
| เทคโนโลยี | วัสดุ | ข้อดี | ใช้สำหรับ |
|---|---|---|---|
| FDM/FFF | Filament | ถูก ง่าย | Prototype, Hobby |
| SLA | Resin | ละเอียดมาก | Jewelry, Dental |
| SLS | Powder | แข็งแรง | Functional parts |
| MJF | Powder + Ink | เร็ว แม่นยำ | Mass production |
| DMLS | Metal powder | โลหะแท้ | Aerospace, Medical |
การใช้งานจริง
อุตสาหกรรม:
 Aerospace: ชิ้นส่วนเครื่องบิน
Aerospace: ชิ้นส่วนเครื่องบิน Medical: Prosthetics, Implants
Medical: Prosthetics, Implants Construction: บ้านพิมพ์ 3D
Construction: บ้านพิมพ์ 3D Automotive: Prototype ชิ้นส่วนรถ
Automotive: Prototype ชิ้นส่วนรถ Fashion: รองเท้า เสื้อผ้า
Fashion: รองเท้า เสื้อผ้า Food: อาหารพิมพ์ 3D
Food: อาหารพิมพ์ 3D
หลักจำ: เครื่องพิมพ์ 3D สร้างวัตถุจริง จากไฟล์ดิจิทัล โดยการวางวัสดุทีละชั้น จนได้รูปทรงสามมิติสมบูรณ์!
คำตอบและวิธีทำ
วิเคราะห์โจทย์
โจทย์ถาม: การกำหนดค่า RAID ข้อใดตอบไม่ถูก ที่มีวัตถุประสงค์:
- ได้ความเร็วในการเข้าถึงดิสก์สูงสุด
- ยอมเสียคุณสมบัติด้านความเชื่อถือได้ไป
คำถามคือหา RAID ระดับไหนที่ไม่ตรงกับคำอธิบายนี้
วิเคราะห์ RAID แต่ละระดับ
a) RAID 0 (Striping) ✓
คุณสมบัติ:
Disk 1: [A1][B1][C1][D1]
Disk 2: [A2][B2][C2][D2]
Disk 3: [A3][B3][C3][D3]
Data A กระจายไป A1, A2, A3
อ่าน/เขียนพร้อมกัน 3 ดิสก์
ข้อดี:
 ความเร็วสูงสุด (อ่าน/เขียนหลายดิสก์พร้อมกัน)
ความเร็วสูงสุด (อ่าน/เขียนหลายดิสก์พร้อมกัน) ใช้พื้นที่เต็ม 100%
ใช้พื้นที่เต็ม 100%
ข้อเสีย:
 ไม่มี redundancy เลย
ไม่มี redundancy เลย ดิสก์เสีย 1 ตัว = ข้อมูลหายหมด
ดิสก์เสีย 1 ตัว = ข้อมูลหายหมด ความเชื่อถือได้ต่ำสุด
ความเชื่อถือได้ต่ำสุด
สรุป: ตรงกับคำอธิบาย - เร็วสุด แต่เสียความเชื่อถือได้
b) RAID 1 (Mirroring) 
คุณสมบัติ:
Disk 1: [A][B][C][D] ← ข้อมูลต้นฉบับ
Disk 2: [A][B][C][D] ← Mirror (คัดลอก)
ข้อดี:
 ความเชื่อถือได้สูง (มีสำรองเต็มชุด)
ความเชื่อถือได้สูง (มีสำรองเต็มชุด) อ่านเร็วขึ้น (อ่านจากดิสก์ใดก็ได้)
อ่านเร็วขึ้น (อ่านจากดิสก์ใดก็ได้) ทนดิสก์เสีย 50% ได้
ทนดิสก์เสีย 50% ได้
ข้อเสีย:
 เขียนช้ากว่า RAID 0 (ต้องเขียน 2 ที่)
เขียนช้ากว่า RAID 0 (ต้องเขียน 2 ที่) ใช้พื้นที่เพียง 50%
ใช้พื้นที่เพียง 50% ไม่ได้ความเร็วสูงสุด
ไม่ได้ความเร็วสูงสุด
สรุป: ไม่ตรงกับคำอธิบาย - เน้นความเชื่อถือได้ ไม่ใช่ความเร็ว
c) RAID 5 (Striping with Parity) 
คุณสมบัติ:
Disk 1: [A1][B1][C1][Dp]
Disk 2: [A2][B2][Cp][D2]
Disk 3: [A3][Bp][C3][D3]
↑
p = parity (สำหรับ recovery)
ข้อดี:
 มี redundancy (parity สำหรับกู้คืน)
มี redundancy (parity สำหรับกู้คืน) ทนดิสก์เสีย 1 ตัวได้
ทนดิสก์เสีย 1 ตัวได้ ความเร็วดี (แต่ไม่เท่า RAID 0)
ความเร็วดี (แต่ไม่เท่า RAID 0) ใช้พื้นที่ประมาณ 67-90% (ขึ้นกับจำนวนดิสก์)
ใช้พื้นที่ประมาณ 67-90% (ขึ้นกับจำนวนดิสก์)
ข้อเสีย:
 เขียนช้ากว่า RAID 0 (ต้องคำนวณ parity)
เขียนช้ากว่า RAID 0 (ต้องคำนวณ parity) ไม่ได้ความเร็วสูงสุด
ไม่ได้ความเร็วสูงสุด
สรุป: ไม่ตรงกับคำอธิบาย - สมดุล ไม่ยอมเสียความเชื่อถือได้
d) RAID 6 (Striping with Double Parity) 
คุณสมบัติ:
Disk 1: [A1][B1][Cp][Dq]
Disk 2: [A2][Bp][C2][Dq]
Disk 3: [Ap][B2][C3][D3]
Disk 4: [Aq][Bq][Cq][D4]
↑ ↑
p, q = parity 2 ชุด
ข้อดี:
 ความเชื่อถือได้สูงสุด
ความเชื่อถือได้สูงสุด ทนดิสก์เสีย 2 ตัวพร้อมกันได้
ทนดิสก์เสีย 2 ตัวพร้อมกันได้ ปลอดภัยมาก
ปลอดภัยมาก
ข้อเสีย:
 เขียนช้าที่สุด (คำนวณ parity 2 ชุด)
เขียนช้าที่สุด (คำนวณ parity 2 ชุด) ใช้พื้นที่น้อยกว่า RAID 5
ใช้พื้นที่น้อยกว่า RAID 5 ตรงข้ามกับคำอธิบายในโจทย์มากที่สุด
ตรงข้ามกับคำอธิบายในโจทย์มากที่สุด
สรุป: ไม่ตรงกับคำอธิบาย - เน้นความเชื่อถือได้มากที่สุด ไม่ใช่ความเร็ว
 ตารางเปรียบเทียบ
ตารางเปรียบเทียบ
| RAID | ความเร็ว | ความเชื่อถือได้ | Redundancy | ตรงกับโจทย์? |
|---|---|---|---|---|
| RAID 0 | ||||
| RAID 1 | ||||
| RAID 5 | ||||
| RAID 6 |
 วิเคราะห์คำถาม
วิเคราะห์คำถาม
โจทย์ถาม: “ข้อใดตอบไม่ถูก”
แปลว่า: ข้อไหนที่ไม่ตรงกับคำอธิบาย
คำอธิบายในโจทย์:
- ✓ ความเร็วสูงสุด
- ✓ ยอมเสียความเชื่อถือได้
ตัวเลือกที่ไม่ตรง:
b) RAID 1:
 ไม่ได้ความเร็วสูงสุด
ไม่ได้ความเร็วสูงสุด ไม่ยอมเสียความเชื่อถือได้ (กลับเน้นความเชื่อถือได้)
ไม่ยอมเสียความเชื่อถือได้ (กลับเน้นความเชื่อถือได้)
c) RAID 5:
 ไม่ได้ความเร็วสูงสุด
ไม่ได้ความเร็วสูงสุด ไม่ยอมเสียความเชื่อถือได้ (มี parity)
ไม่ยอมเสียความเชื่อถือได้ (มี parity)
d) RAID 6:
 ไม่ได้ความเร็วสูงสุด (ช้าที่สุดในกลุ่มนี้)
ไม่ได้ความเร็วสูงสุด (ช้าที่สุดในกลุ่มนี้) ไม่ยอมเสียความเชื่อถือได้ (เน้นความเชื่อถือได้มากที่สุด)
ไม่ยอมเสียความเชื่อถือได้ (เน้นความเชื่อถือได้มากที่สุด) ตรงข้ามกับโจทย์ทุกประการ
ตรงข้ามกับโจทย์ทุกประการ
 เทคนิคจำ RAID
เทคนิคจำ RAID
จำแบบง่าย
RAID 0:
- 0 = Zero redundancy (ไม่มีสำรอง)
- เร็วสุด แต่เสี่ยงสุด
RAID 1:
- 1 = One mirror (กระจก 1 บาน)
- ปลอดภัย แต่ไม่เร็วสุด
RAID 5:
- 5 = ต้องมีดิสก์อย่างน้อย 3 ตัว
- สมดุล (ไม่เร็วสุด ไม่ปลอดภัยสุด)
RAID 6:
- 6 = RAID 5 + อีก 1 parity
- ปลอดภัยสุด แต่ช้ากว่า
ตารางสรุป
| Feature | RAID 0 | RAID 1 | RAID 5 | RAID 6 |
|---|---|---|---|---|
| Min disks | 2 | 2 | 3 | 4 |
| Speed | ||||
| Safety | ||||
| Capacity | 100% | 50% | 67-90% | 50-80% |
| Fault tolerance | 0 | 1 disk | 1 disk | 2 disks |
 เทคนิคหาคำตอบแบบรวดเร็ว
เทคนิคหาคำตอบแบบรวดเร็ว
ขั้นตอน:
1. อ่านโจทย์: เน้นความเร็ว + ยอมเสียความเชื่อถือได้
2. หา RAID ที่ตรง: RAID 0 เท่านั้น
3. หา RAID ที่ไม่ตรง: ทุกข้ออื่นไม่ตรง
4. หา RAID ที่ไม่ตรงมากที่สุด:
- RAID 6 เน้นความเชื่อถือได้มากที่สุด
- ช้าที่สุด (เพราะ double parity)
- ตรงข้ามกับโจทย์ทุกประการ
คำตอบ: d) RAID 6 
เหตุผล:
RAID 6 ตรงข้ามกับคำอธิบายในโจทย์มากที่สุด เพราะ:
 ไม่ได้ความเร็วสูงสุด - กลับช้าที่สุดในกลุ่มนี้
ไม่ได้ความเร็วสูงสุด - กลับช้าที่สุดในกลุ่มนี้ ไม่ยอมเสียความเชื่อถือได้ - กลับเน้นเพิ่มความเชื่อถือได้สูงสุด
ไม่ยอมเสียความเชื่อถือได้ - กลับเน้นเพิ่มความเชื่อถือได้สูงสุด มี double parity ทำให้เขียนช้า
มี double parity ทำให้เขียนช้า ทนดิสก์เสีย 2 ตัวพร้อมกัน (ปลอดภัยสุด)
ทนดิสก์เสีย 2 ตัวพร้อมกัน (ปลอดภัยสุด)
ตัวเลือกอื่น:
- a) RAID 0 → ตรงกับโจทย์ - เร็วสุด ไม่มี redundancy
- b) RAID 1 → ไม่ตรง - แต่ยังมีความเร็วอ่านที่ดี
- c) RAID 5 → ไม่ตรง - แต่ยังสมดุลระหว่างเร็วและปลอดภัย
 สรุปสำคัญ
สรุปสำคัญ
ถ้าต้องการ:
ความเร็วสูงสุด (ยอมเสียความปลอดภัย):
→ RAID 0 ![]()
ความปลอดภัยสูง (ยอมเสียความเร็ว):
→ RAID 1 หรือ RAID 6 ![]()
สมดุล:
→ RAID 5 ![]()
หลักจำ: RAID 0 = เร็วแต่เสี่ยง, RAID 6 = ปลอดภัยแต่ช้า (ตรงข้ามกัน)!
คำตอบที่ถูกต้องคือ c) ระบบคู่ขนาน, ระบบโคลด์สแตนด์บาย, ระบบเครื่องเดียว
การเรียงลำดับสภาพพร้อมใช้งาน (\text{Availability}) จาก มากที่สุดไปน้อยที่สุด คือ \text{Dual System} \rightarrow \text{Cold Standby System} \rightarrow \text{Simplex System}
การวิเคราะห์สภาพพร้อมใช้งาน (\text{Availability})
สภาพพร้อมใช้งาน (\text{Availability}) คือ ความสามารถของระบบในการทำงานอย่างต่อเนื่องในช่วงเวลาที่กำหนด (\text{uptime}). ระบบที่มีความซ้ำซ้อน (\text{Redundancy}) สูงกว่าจะมี \text{Availability} สูงกว่า
1. ระบบคู่ขนาน (\text{Dual System}) - \text{สูงสุด}
- ลักษณะ: มีคอมพิวเตอร์ทำงานพร้อมกัน 2 ชุด (\text{Active-Active} หรือ \text{Active-Standby} ที่สลับการทำงานได้เร็วมาก)
- Availability: สูงที่สุด เพราะเมื่อเครื่องหนึ่งล้มเหลว อีกเครื่องหนึ่งสามารถ รับช่วงการทำงานต่อได้ทันที (\text{Immediate Failover}) ทำให้ผู้ใช้แทบไม่รู้สึกว่าระบบล้มเหลวเลย
2. ระบบโคลด์สแตนด์บาย (\text{Cold Standby System}) - \text{ปานกลาง}
- ลักษณะ: มีคอมพิวเตอร์ชุดหลักทำงานอยู่ (\text{Active}) และมีคอมพิวเตอร์สำรองอีกชุดที่ ปิดอยู่ หรือ พร้อมทำงานแต่ไม่ได้รันแอปพลิเคชันหลัก (\text{Standby}).
- Availability: ปานกลาง เพราะเมื่อเครื่องหลักล้มเหลว จะต้องใช้ เวลาในการเปิดเครื่องสำรอง, โหลดระบบปฏิบัติการ, และเริ่มต้นแอปพลิเคชันต่างๆ (\text{Recovery Time}) ซึ่งใช้เวลานานกว่าระบบคู่ขนาน
3. ระบบเครื่องเดียว (\text{Simplex System}) - \text{ต่ำที่สุด}
- ลักษณะ: มีคอมพิวเตอร์ทำงานเพียง 1 ชุด เท่านั้น (\text{No Redundancy}).
- Availability: ต่ำที่สุด เพราะเมื่อเครื่องล้มเหลว จะต้องใช้เวลาในการซ่อมแซมหรือเปลี่ยนเครื่องใหม่ทั้งหมด ก่อนที่ระบบจะกลับมาใช้งานได้อีกครั้ง
ดังนั้น การเรียงลำดับจาก \text{Availability} มากที่สุดไปน้อยที่สุดคือ: \text{Dual System} \rightarrow \text{Cold Standby System} \rightarrow \text{Simplex System}
คำตอบและวิธีทำ
วิเคราะห์โจทย์
ข้อมูลที่ให้:
- เครื่องพิมพ์พิมพ์ได้ 400 ตัวอักษร/วินาที
- ใช้ interrupt-driven I/O
- Interrupt handler ใช้เวลา 50 ไมโครวินาที (μs) ต่อครั้ง
- ถาม: % เวลาว่างที่ CPU ทำงานอื่นได้
วิธีแก้ทีละขั้นตอน
ขั้นที่ 1: คำนวณเวลาต่อ 1 ตัวอักษร
ความเร็วพิมพ์ = 400 ตัวอักษร/วินาที
เวลาต่อ 1 ตัวอักษร = 1/400 วินาที
= 0.0025 วินาที
= 2,500 ไมโครวินาที (μs)
ขั้นที่ 2: วิเคราะห์ Interrupt
ทุกๆ 1 ตัวอักษร:
- ต้องมี interrupt 1 ครั้ง (เพื่อรับตัวอักษร)
- Interrupt ใช้เวลา 50 μs
- เวลารอบหนึ่ง = 2,500 μs
Timeline สำหรับ 1 ตัวอักษร:
[────────────── 2,500 μs ──────────────]
[Interrupt: 50 μs][CPU ว่าง: 2,450 μs]
ขั้นที่ 3: คำนวณ % เวลา interrupt
% เวลาที่ใช้กับ interrupt = (เวลา interrupt / เวลาทั้งหมด) × 100
= (50 / 2,500) × 100
= 0.02 × 100
= 2%
ขั้นที่ 4: คำนวณ % เวลาว่าง
% เวลาว่างสำหรับทำงานอื่น = 100% - 2%
= 98%
 วิธีคำนวณแบบทางลัด
วิธีคำนวณแบบทางลัด
เทคนิค 1: คำนวณต่อวินาที
จำนวน interrupt/วินาที = 400 ครั้ง (ตัวอักษร 400 ตัว)
เวลา interrupt ทั้งหมด/วินาที:
= 400 × 50 μs
= 20,000 μs
= 0.02 วินาที
% interrupt overhead = (0.02/1) × 100 = 2%
% เวลาว่าง = 100 - 2 = 98%
เทคนิค 2: สูตรโดยตรง
% CPU Available = 100 × [1 - (Interrupt_frequency × Interrupt_time)]
= 100 × [1 - (400/sec × 50×10⁻⁶ sec)]
= 100 × [1 - 0.02]
= 100 × 0.98
= 98%
 ภาพประกอบ Timeline
ภาพประกอบ Timeline
ใน 1 วินาที:
วินาทีที่ 1:
├─[I]─[CPU ทำงานอื่น]─[I]─[CPU ทำงานอื่น]─[I]─...─[I]─┤
↑ ↑
50μs 2,450μs
I = Interrupt (50 μs)
มี 400 ครั้งใน 1 วินาที
เวลา interrupt รวม = 400 × 50 μs = 20,000 μs = 0.02 sec
เวลาว่าง = 1 - 0.02 = 0.98 sec = 98%
 เทคนิคจำแบบง่าย
เทคนิคจำแบบง่าย
สูตรสำคัญ
% CPU Overhead = (Interrupts/sec × Time/interrupt) × 100
% CPU Available = 100% - % Overhead
วิธีคิด 3 ขั้นตอน
1️⃣ หาว่ามี interrupt กี่ครั้งต่อวินาที
= ความเร็ว I/O (ในที่นี้ = 400)
2️⃣ คูณด้วยเวลาต่อ interrupt
= 400 × 50 μs = 20,000 μs = 0.02 sec
3️⃣ เอา 1 - ผลลัพธ์ แล้วคูณ 100
= (1 - 0.02) × 100 = 98%
 ตารางสรุป
ตารางสรุป
| รายการ | ค่า | หน่วย |
|---|---|---|
| ความเร็วพิมพ์ | 400 | ตัวอักษร/วินาที |
| เวลาต่อตัวอักษร | 2,500 | μs |
| เวลา interrupt | 50 | μs |
| % interrupt overhead | 2 | % |
| % CPU ว่าง | 98 | % |
 ตรวจสอบคำตอบ
ตรวจสอบคำตอบ
วิธีตรวจสอบ 1: ใน 1 วินาที
เวลาทั้งหมด = 1,000,000 μs (1 วินาที)
เวลา interrupt = 400 × 50 = 20,000 μs
เวลาว่าง = 1,000,000 - 20,000 = 980,000 μs
% = (980,000 / 1,000,000) × 100 = 98% ✅
วิธีตรวจสอบ 2: ต่อรอบ
รอบหนึ่ง = 2,500 μs
ใช้ไป = 50 μs
เหลือ = 2,450 μs
% = (2,450 / 2,500) × 100 = 98% ✅
คำตอบ: a) 98 
สรุปการคำนวณ:
ขั้นตอนสั้น:
- จำนวน interrupt = 400 ครั้ง/วินาที
- เวลา interrupt รวม = 400 × 50 μs = 20,000 μs = 0.02 วินาที
- % interrupt = 2%
- % เวลาว่าง = 98%
ความหมาย:
- CPU ใช้เวลา 2% ในการจัดการ interrupt
- CPU มีเวลาว่าง 98% สำหรับทำงานอื่น
- เครื่องพิมพ์ไม่ได้กิน CPU มากนัก เพราะ I/O ช้ากว่า CPU มาก
 ข้อมูลเพิ่มเติม
ข้อมูลเพิ่มเติม
ทำไม Interrupt-driven I/O ถึงมีประสิทธิภาพ?
เปรียบเทียบ:
1. Polling (ถามซ้ำๆ):
CPU: "เสร็จหรือยัง?" (ถามตลอด)
Printer: "ยัง..."
CPU: "เสร็จหรือยัง?"
Printer: "ยัง..."
→ เสีย CPU 100%!
2. Interrupt-driven:
CPU: ทำงานอื่น...
Printer: "เสร็จแล้ว!" (ส่ง interrupt)
CPU: จัดการ (50 μs) แล้วกลับไปทำงานอื่น
→ เสีย CPU เพียง 2%!
สูตรทั่วไป
% CPU Overhead = (I/O_rate × Interrupt_time) × 100
% CPU Available = 100 - % Overhead
ตัวอย่าง:
- Disk: 1000 interrupts/sec × 10 μs = 1% overhead
- Network: 10000 packets/sec × 5 μs = 5% overhead
- Keyboard: 10 keys/sec × 100 μs = 0.001% overhead
หลักจำ: I/O ยิ่งช้า (เช่น เครื่องพิมพ์) → interrupt น้อย → overhead ต่ำ → CPU ว่างมาก!
คำตอบและวิธีทำ
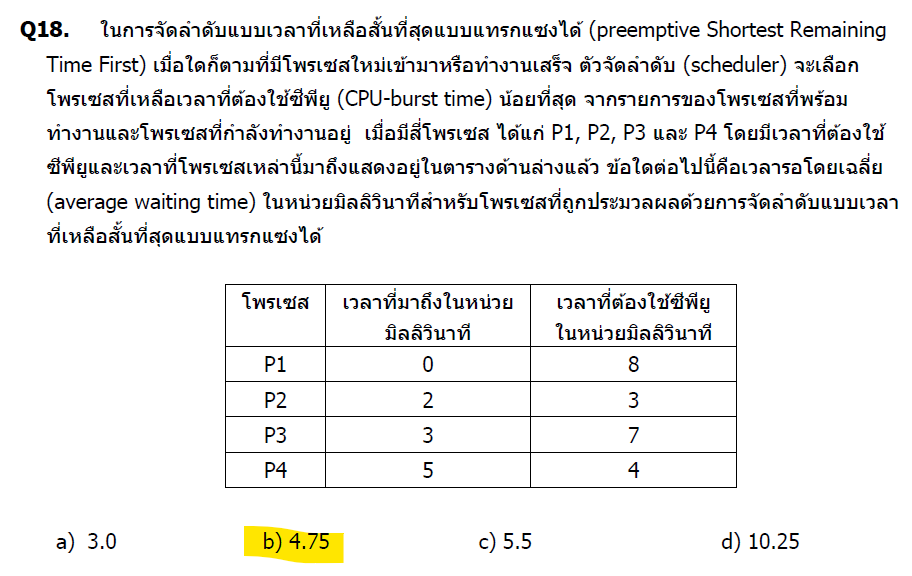
วิเคราะห์โจทย์
Algorithm: Preemptive Shortest Remaining Time First (SRTF)
- เลือก process ที่มี remaining time น้อยที่สุด
- สามารถ preempt (แย่งชิง) ได้
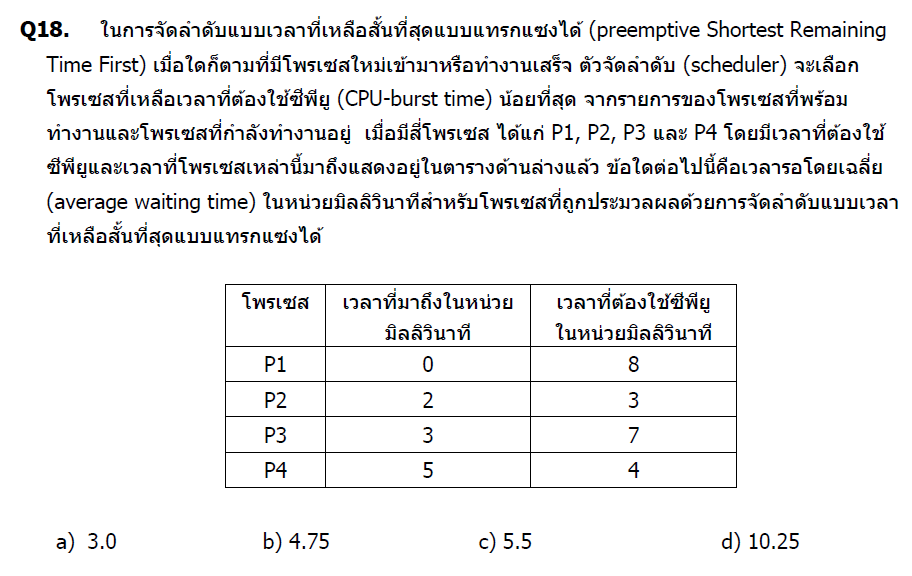
ข้อมูล:
| Process | Arrival | Burst |
|---|---|---|
| P1 | 0 | 8 |
| P2 | 2 | 3 |
| P3 | 3 | 7 |
| P4 | 5 | 4 |
ถาม: Average Waiting Time
วิธีแก้: จำลอง SRTF Scheduling
Timeline การทำงาน
Time 0-2:
Available: P1 (remaining: 8)
Run: P1
- P1 ทำงาน 2 หน่วย
- P1 remaining = 8 - 2 = 6
Time 2:
P2 arrives (burst: 3)
Available: P1(6), P2(3)
Compare: 6 vs 3
Run: P2 ← เลือก P2 (shortest)
- Preempt P1 (แย่ง P1 ออก)
Time 2-3:
Run: P2 (3 หน่วย)
- P2 ทำงาน 1 หน่วย
- P2 remaining = 3 - 1 = 2
Time 3:
P3 arrives (burst: 7)
Available: P1(6), P2(2), P3(7)
Compare: 6 vs 2 vs 7
Run: P2 ← ยังเป็น P2 (shortest)
Time 3-5:
Run: P2
- P2 ทำงานต่ออีก 2 หน่วย
- P2 เสร็จที่ time 5 ✓
Time 5:
P4 arrives (burst: 4)
Available: P1(6), P3(7), P4(4)
Compare: 6 vs 7 vs 4
Run: P4 ← เลือก P4 (shortest)
Time 5-9:
Run: P4
- P4 ทำงาน 4 หน่วย
- P4 เสร็จที่ time 9 ✓
Time 9:
Available: P1(6), P3(7)
Compare: 6 vs 7
Run: P1 ← เลือก P1 (shortest)
Time 9-15:
Run: P1
- P1 ทำงานต่ออีก 6 หน่วย
- P1 เสร็จที่ time 15 ✓
Time 15-22:
Available: P3(7)
Run: P3
- P3 ทำงาน 7 หน่วย
- P3 เสร็จที่ time 22 ✓
Gantt Chart
0────2────5────9────15────22
│ P1 │ P2 │ P4 │ P1 │ P3 │
คำนวณ Waiting Time
สูตร:
Waiting Time = Turnaround Time - Burst Time
Turnaround Time = Completion Time - Arrival Time
P1:
Arrival: 0
Completion: 15
Turnaround: 15 - 0 = 15
Burst: 8
Waiting: 15 - 8 = 7
P2:
Arrival: 2
Completion: 5
Turnaround: 5 - 2 = 3
Burst: 3
Waiting: 3 - 3 = 0
P3:
Arrival: 3
Completion: 22
Turnaround: 22 - 3 = 19
Burst: 7
Waiting: 19 - 7 = 12
P4:
Arrival: 5
Completion: 9
Turnaround: 9 - 5 = 4
Burst: 4
Waiting: 4 - 4 = 0
ตารางสรุป
| Process | Arrival | Burst | Completion | Turnaround | Waiting |
|---|---|---|---|---|---|
| P1 | 0 | 8 | 15 | 15 | 7 |
| P2 | 2 | 3 | 5 | 3 | 0 |
| P3 | 3 | 7 | 22 | 19 | 12 |
| P4 | 5 | 4 | 9 | 4 | 0 |
คำนวณค่าเฉลี่ย
Average Waiting Time = (7 + 0 + 12 + 0) / 4
= 19 / 4
= 4.75
คำตอบ: b) 4.75 
 เทคนิคทำโจทย์ SRTF
เทคนิคทำโจทย์ SRTF
ขั้นตอนการทำ:
1. เรียงตาม Arrival Time
P1(0) → P2(2) → P3(3) → P4(5)
2. จำลอง Timeline:
- ทุกครั้งที่มี process มาถึง → เปรียบเทียบ remaining time
- เลือก process ที่ remaining time น้อยที่สุด
- ถ้ามี process ใหม่ที่ remaining time น้อยกว่า → preempt
3. บันทึก Completion Time ของแต่ละ process
4. คำนวณ Waiting Time:
Waiting = (Completion - Arrival) - Burst
5. หาค่าเฉลี่ย
 เทคนิคลัด: ใช้ตาราง
เทคนิคลัด: ใช้ตาราง
| Time | Event | Available (Remaining) | Selected | Reason |
|---|---|---|---|---|
| 0 | P1 arrives | P1(8) | P1 | Only one |
| 2 | P2 arrives | P1(6), P2(3) | P2 | 3 < 6 |
| 3 | P3 arrives | P1(6), P2(2), P3(7) | P2 | 2 < 6 < 7 |
| 5 | P2 done, P4 arrives | P1(6), P3(7), P4(4) | P4 | 4 < 6 < 7 |
| 9 | P4 done | P1(6), P3(7) | P1 | 6 < 7 |
| 15 | P1 done | P3(7) | P3 | Only one |
| 22 | P3 done | - | - | All done |
 Timeline รายละเอียด
Timeline รายละเอียด
Time: 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22
CPU: P1 P1 P2 P2 P2 P4 P4 P4 P4 P1 P1 P1 P1 P1 P1 P3 P3 P3 P3 P3 P3 P3
└─┘ └────┘ └──────┘ └──────────┘ └─────────────────────┘
2 3 4 6 7
P1: 0-2 (work 2), idle 2-9, 9-15 (work 6) → waiting = 7
P2: arrive 2, 2-5 (work 3) → waiting = 0
P3: arrive 3, idle 3-15, 15-22 (work 7) → waiting = 12
P4: arrive 5, 5-9 (work 4) → waiting = 0
 วิธีตรวจสอบคำตอบ
วิธีตรวจสอบคำตอบ
ตรวจสอบ waiting time ทีละตัว:
P1 waiting = 7?
ช่วงรอ: [2-9] = 7 หน่วย ✓
(รอเพราะถูก preempt โดย P2 และ P4)
P2 waiting = 0?
Arrive 2 → Run ทันที 2-5 → ไม่รอเลย ✓
P3 waiting = 12?
Arrive 3 → รอจนถึง 15 = 12 หน่วย ✓
(รอเพราะ P2, P4, P1 ทำก่อน)
P4 waiting = 0?
Arrive 5 → Run ทันที 5-9 → ไม่รอเลย ✓
Average:
(7 + 0 + 12 + 0) / 4 = 4.75 ✓
 สรุปสำคัญ
สรุปสำคัญ
SRTF คุณสมบัติ:
![]() Optimal - Average waiting time ต่ำสุด (ในกลุ่ม preemptive)
Optimal - Average waiting time ต่ำสุด (ในกลุ่ม preemptive)
![]() Preemptive - สามารถแย่งชิงได้
Preemptive - สามารถแย่งชิงได้
![]() Starvation - process ที่ burst ยาวอาจรอนาน
Starvation - process ที่ burst ยาวอาจรอนาน
![]() Overhead - ต้องคำนวณ remaining time บ่อย
Overhead - ต้องคำนวณ remaining time บ่อย
เปรียบเทียบกับ SJF:
- SJF (Non-preemptive): ไม่แย่งชิง
- SRTF (Preemptive SJF): แย่งชิงได้ → Average WT ดีกว่า
หลักจำ: SRTF = เลือก remaining time น้อยสุด + สามารถ preempt ได้!
คำตอบที่ถูกต้องคือ b) 4.75
คำถามนี้ต้องการหา **เวลาคอยเฉลี่ย (\text{Average Waiting Time}) ** โดยใช้การจัดลำดับแบบ เวลาที่เหลือสั้นที่สุดแบบแทรกแซงได้ (\text{Preemptive Shortest Remaining Time First - PSRTF} หรือ \text{SRTF})
วิธีทำ: การคำนวณเวลาคอยเฉลี่ย (\text{Average Waiting Time})
การจัดลำดับแบบ \text{SRTF} คือการที่ \text{Scheduler} จะเลือกทำงานกับโปรเซสที่มีเวลา \text{CPU} ที่เหลือ (Remaining Time) น้อยที่สุด ณ ขณะนั้น และสามารถแทรกแซง (\text{Preempt}) โปรเซสที่กำลังทำงานอยู่ได้ เมื่อมีโปรเซสใหม่เข้ามาและมี \text{Remaining Time} น้อยกว่า
| โปรเซส (\text{P}) | เวลาที่มาถึง (\text{AT}) | เวลาที่ต้องการใช้ \text{CPU} (\text{BT}) |
|---|---|---|
| \text{P1} | 0 | 8 |
| \text{P2} | 2 | 3 |
| \text{P3} | 3 | 7 |
| \text{P4} | 5 | 4 |
1. แผนผังแกนต์ (\text{Gantt Chart})
| เวลา (ms) | สถานะ | โปรเซสที่ทำงาน | \text{Remaining Time} | หมายเหตุ |
|---|---|---|---|---|
| 0 | (\text{P1} มาถึง) | \text{P1} (8) | \text{P1: 8} | |
| 0-2 | \text{P1} | \text{P1: 6} | ||
| 2 | (\text{P2} มาถึง) | \text{P2} (3) | \text{P1: 6, P2: 3} | \text{P2} สั้นกว่า \text{P1} จึง \text{Preempt} \text{P1} |
| 2-3 | \text{P2} | \text{P1: 6, P2: 2} | ||
| 3 | (\text{P3} มาถึง) | \text{P2} (2) | \text{P1: 6, P2: 2, P3: 7} | \text{P2} สั้นที่สุด |
| 3-5 | \text{P2} | \text{P1: 6, P2: 0, P3: 7} | \text{P2} เสร็จสิ้นที่ \text{t=5} | |
| 5 | (\text{P4} มาถึง) | \text{P4} (4) | \text{P1: 6, P3: 7, P4: 4} | \text{P4} สั้นที่สุด |
| 5-9 | \text{P4} | \text{P1: 6, P3: 7, P4: 0} | \text{P4} เสร็จสิ้นที่ \text{t=9} | |
| 9 | \text{P1} (6) | \text{P1: 6, P3: 7} | \text{P1} สั้นกว่า \text{P3} | |
| 9-15 | \text{P1} | \text{P1: 0, P3: 7} | \text{P1} เสร็จสิ้นที่ \text{t=15} | |
| 15-22 | \text{P3} (7) | \text{P3: 0} | \text{P3} เสร็จสิ้นที่ \text{t=22} |
สรุปแผนผังแกนต์:
| \text{P1} | \text{P2} | \text{P2} | \text{P4} | \text{P1} | \text{P3} |
|---|---|---|---|---|---|
| 0-2 | 2-3 | 3-5 | 5-9 | 9-15 | 15-22 |
2. คำนวณเวลาที่ใช้ในการประมวลผลทั้งหมด (\text{Turnaround Time})
$$\text{Turnaround Time (TT)} = \text{เวลาสิ้นสุด} - \text{เวลาที่มาถึง}$$
- \text{P1}: \text{TT1} = 15 - 0 = 15
- \text{P2}: \text{TT2} = 5 - 2 = 3
- \text{P3}: \text{TT3} = 22 - 3 = 19
- \text{P4}: \text{TT4} = 9 - 5 = 4
3. คำนวณเวลาคอย (\text{Waiting Time})
$$\text{Waiting Time (WT)} = \text{Turnaround Time} - \text{เวลาที่ต้องการใช้ } \text{CPU}$$
- \text{P1}: \text{WT1} = 15 - 8 = 7
- \text{P2}: \text{WT2} = 3 - 3 = 0
- \text{P3}: \text{WT3} = 19 - 7 = 12
- \text{P4}: \text{WT4} = 4 - 4 = 0
รวมเวลาคอยทั้งหมด: \text{Total WT} = 7 + 0 + 12 + 0 = 19 ms
4. คำนวณเวลาคอยเฉลี่ย (\text{Average Waiting Time})
$$\text{Average Waiting Time} = \frac{\text{Total Waiting Time}}{\text{จำนวนโปรเซส}}$$
$$\text{Average Waiting Time} = \frac{19}{4} = 4.75 \text{ มิลลิวินาที}$$
คำตอบที่ถูกต้องคือ d) เฉพาะไฟล์ที่มีข้อมูลระบุว่ามีการแก้ไขไฟล์เท่านั้นที่จะถูกสำรอง และข้อมูลที่ระบุว่ามีการแก้ไขไฟล์นั้นจะถูกรีเซ็ต
การวิเคราะห์วิธีการสำรองข้อมูลแบบเพิ่มส่วน (\text{Incremental Backup})
\text{Incremental Backup} (การสำรองข้อมูลแบบเพิ่มส่วน) เป็นวิธีการสำรองข้อมูลที่มุ่งเน้นการเก็บเฉพาะการเปลี่ยนแปลงที่เกิดขึ้นหลังจากรอบการสำรองข้อมูลครั้งล่าสุดเท่านั้น เทคนิคนี้มีจุดประสงค์เพื่อประหยัดพื้นที่จัดเก็บและลดเวลาที่ใช้ในการสำรองข้อมูล
กลไกการทำงาน
- การสำรองข้อมูล: ระบบจะทำการสำรองข้อมูล เฉพาะไฟล์ที่ถูกแก้ไข นับตั้งแต่การสำรองข้อมูลแบบเต็ม (\text{Full Backup}) หรือการสำรองแบบเพิ่มส่วน (\text{Incremental Backup}) ครั้งล่าสุด โดยอ้างอิงจาก \text{Archive Bit} (บิตระบุการเก็บถาวร) ซึ่งเป็น \text{flag} สถานะของไฟล์
- การจัดการ \text{Archive Bit}:
- เมื่อไฟล์ถูกสร้างหรือแก้ไข ระบบปฏิบัติการจะ ตั้งค่า \text{Archive Bit} เป็น \text{ON} (หรือ \text{Set}) เพื่อระบุว่าไฟล์นี้ต้องการการสำรองข้อมูล
- เมื่อโปรแกรมสำรองข้อมูลทำการสำรองไฟล์นั้นเสร็จสิ้นแล้ว จะต้อง รีเซ็ต (\text{Clear}) \text{Archive Bit} เป็น \text{OFF} เพื่อระบุว่าไฟล์นี้ถูกสำรองไปแล้ว และพร้อมสำหรับการเปลี่ยนแปลงครั้งถัดไป
การวิเคราะห์ตัวเลือก
| ตัวเลือก | การสำรองข้อมูล | การจัดการ \text{Archive Bit} | สอดคล้องกับ \text{Incremental Backup} |
|---|---|---|---|
| a) \text{ไฟล์ทั้งหมด...} | ผิด (ถ้าทั้งหมดจะกลายเป็น \text{Full Backup}) | \text{คงไว้ดังเดิม} | ผิด |
| b) \text{ไฟล์ทั้งหมด...} | ผิด | \text{ถูกรีเซ็ต} | ผิด |
| c) \text{เฉพาะไฟล์ที่ถูกแก้ไขเท่านั้น} | ถูกต้อง | \text{คงไว้ดังเดิม} | ผิด (ถ้าไม่รีเซ็ต จะสำรองไฟล์เดิมซ้ำในการสำรองครั้งถัดไป) |
| d) \text{เฉพาะไฟล์ที่ถูกแก้ไขเท่านั้น} | ถูกต้อง | \text{ถูกรีเซ็ต} | ถูกต้อง (เป็นการเตรียมพร้อมสำหรับการเปลี่ยนแปลงครั้งต่อไป) |
ดังนั้น \text{Incremental Backup} จะสำรอง เฉพาะไฟล์ที่มีการแก้ไข (ซึ่งดูจาก \text{Archive Bit} ที่ \text{Set}) และ รีเซ็ต \text{Archive Bit} นั้น เพื่อรอการแก้ไขใหม่