คำตอบที่ถูกต้องคือ b) 7,500
วิเคราะห์ทีละขั้น
ข้อมูลที่ให้มา:
- ราคาขายต่อหน่วย = $50
- อัตราต้นทุนผันแปร (Variable cost ratio) = 60%
→ ต้นทุนผันแปรต่อหน่วย = 0.6 × 50 = $30 - ต้นทุนคงที่ = $100,000
- ต้องการกำไร = $50,000
สูตรพื้นฐาน
\text{ยอดขาย (จำนวนหน่วย)} = \frac{\text{ต้นทุนคงที่ + กำไรที่ต้องการ}}{\text{ราคาขายต่อหน่วย} - \text{ต้นทุนผันแปรต่อหน่วย}}
แทนค่า:
= \frac{100,000 + 50,000}{50 - 30} = \frac{150,000}{20} = 7,500
คำตอบ: b) 7,500 หน่วย
มาวิเคราะห์โจทย์นี้กันครับ 
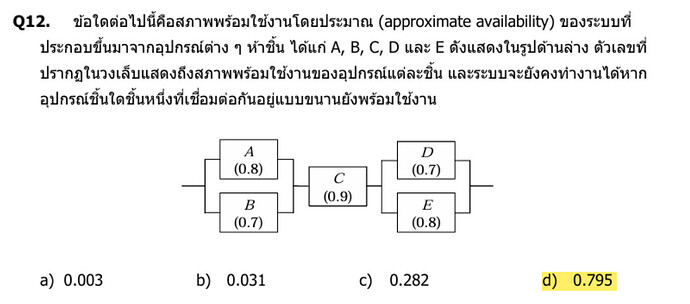
โจทย์ถามหา ค่าความพร้อมใช้งานโดยประมาณ (approximate availability) ของระบบที่ประกอบจากอุปกรณ์ A, B, C, D, E
โดยวงจรในภาพแสดงว่า:
- A และ B ต่อกันแบบ ขนาน (Parallel)
- C ต่อ อนุกรม (Series) กับกลุ่ม (A,B) และ (D,E)
- D และ E ต่อกันแบบ ขนาน (Parallel)
ดังนั้นโครงสร้างระบบคือ
(A || B) – C – (D || E)
ขั้นตอนการคำนวณ:
ความพร้อมของ A||B (ขนาน)
สูตรขนาน:
A_{AB} = 1 - (1 - A_A)(1 - A_B)
แทนค่า:
A_{AB} = 1 - (1 - 0.8)(1 - 0.7)
= 1 - (0.2)(0.3)
= 1 - 0.06 = 0.94
ความพร้อมของ D||E (ขนาน)
A_{DE} = 1 - (1 - 0.7)(1 - 0.8) = 1 - (0.3)(0.2) = 1 - 0.06 = 0.94
ระบบเป็นอนุกรมระหว่าง (A||B), C, (D||E)
สูตรอนุกรม:
A_{total} = A_{AB} \times A_C \times A_{DE}
แทนค่า:
A_{total} = 0.94 \times 0.9 \times 0.94
= 0.94^2 \times 0.9
= 0.8836 \times 0.9
= 0.79524
คำตอบที่ถูกต้องคือ
d) 0.795
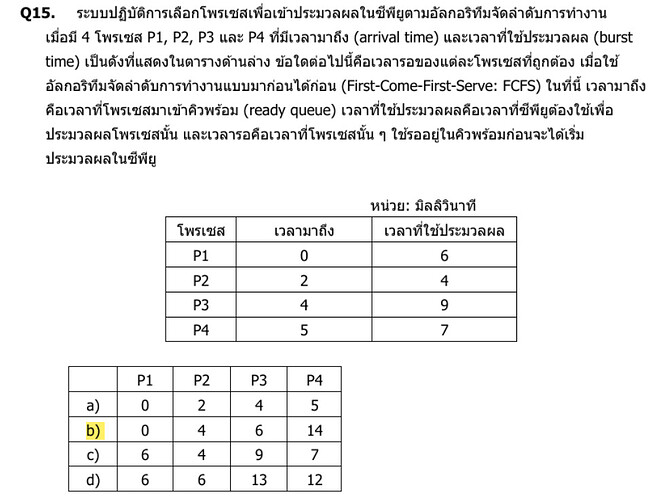
คำตอบที่ถูก: b) 0 4 6 14
อธิบายสั้น ๆ (FCFS):
- P1 เริ่มที่เวลา 0 ⇒ รอ 0
- P2 มาถึง 2 เริ่มหลัง P1 จบที่ 6 ⇒ รอ 6−2 = 4
- P3 มาถึง 4 เริ่มที่ 10 ⇒ รอ 10−4 = 6
- P4 มาถึง 5 เริ่มที่ 19 ⇒ รอ 19−5 = 14
มาวิเคราะห์ทีละขั้นครับ
โจทย์:
- หน่วยความจำ = (512 \times 10^6) ไบต์
- เก็บสัญญาณเสียงแบบ 8-bit (1 byte) ต่อ sample
- Sampling rate = 11,000 ครั้งต่อวินาที
คำนวณจำนวน sample ทั้งหมดที่เก็บได้
512 \times 10^6 \text{ bytes} = 512 \times 10^6 \text{ samples}
คำนวณระยะเวลาที่เก็บได้
\text{เวลา (วินาที)} = \frac{\text{จำนวน sample ทั้งหมด}}{\text{sampling rate}} = \frac{512 \times 10^6}{11,000} = 46545.45\ \text{วินาที}
แปลงเป็น “นาที”
46545.45 \div 60 = 775.76\ \text{นาที}
คำตอบที่ถูกต้องคือ:
c) 775 นาที
ตอบ: b) 6
อธิบาย: ชั่วโมงการทำงานทั้งหมดใน 360 วัน = 360 \times 24 = 8{,}640 ชั่วโมง
จำนวนครั้งเสียเฉลี่ย = เวลาทำงานทั้งหมด / MTBF = 8{,}640 / 1{,}440 = 6 ครั้ง.
ตอบ: c) 70
โจทย์เป็นการหากำไรสูงสุด (Linear Programming)
ให้ (x) = จำนวนสินค้า X, (y) = จำนวนสินค้า Y
เงื่อนไขวัตถุดิบ:
- A: 2x + y \le 100
- B: x + 2y \le 80
กำไร: Z = 1x + 1.5y
พิจารณาจุดมุม:
- (x, y) = (50, 0) → Z = 50
- (0, 40) → Z = 60
- จุดตัด 2x + y = 100 และ x + 2y = 80 ⇒ x=40, y=20
⇒ Z = 40 + 1.5(20) = 70
ดังนั้นกำไรสูงสุด = 70 ดอลลาร์.
